Esercitazione 2
Errori comuni: i corto circuiti
Vediamo ora un esempio di come non tenere presente la corrispondenza tra Verilog e schemi circuitali porta a grossi guai.
La maggior parte di quello di cui discutiamo in questo corso si applica per qualunque tecnologia si utilizzi per implementarle. Infatti, una volta ottenuti gli operatori logici elementari, sono identici i passaggi necessari per arrivare a costruire un processore in grado di eseguire programmi. Per esempio, c'è chi ha realizzato un processore funzionante usando la redstone di Minecraft, così come ricerca sull'uso della luce, detta photonic computing.
Attualmente, usiamo elettronica digitale basata su semiconduttori (studiata nel corso di Elettronica Digitale). Questo implica che dobbiamo stare attenti ai limiti imposti dall'elettronica quando realizziamo reti logiche, in particolare il fatto che non si possono collegare due o più fonti di tensione allo stesso filo. Vediamo perché.
Una porta logica agisce fondamentalmente come un interruttore che collega la propria uscita a terra, , o alla tensione di alimentazione Vcc, per esempio . All'ingresso di una porta logica, invece, viene rilevata la tensione senza contatti elettrici con l'uscita.
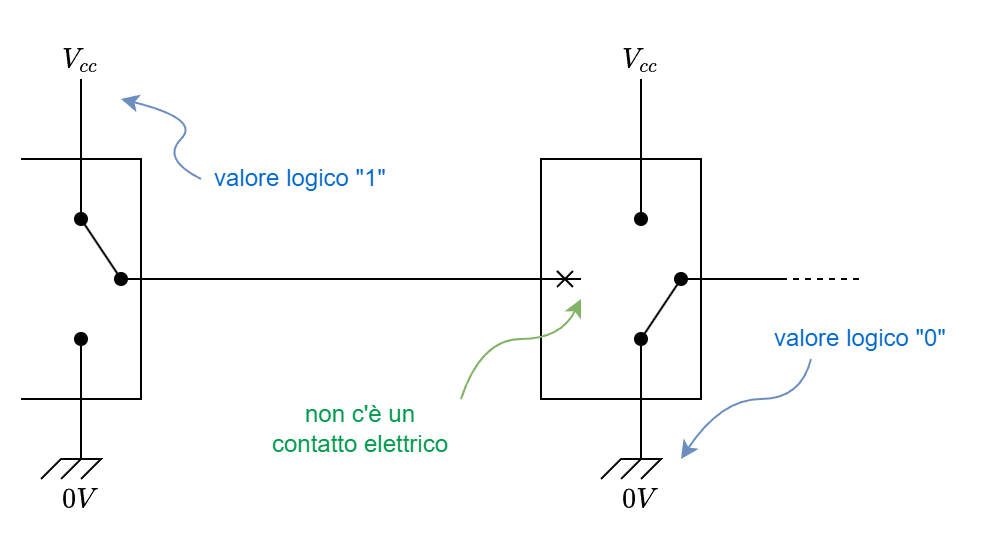
Cosa succede invece se colleghiamo le uscite di due porte logiche, in particolare se una produce 1 e l'altra 0? Si chiude un circuito che collega Vcc a terra. Data la differenza di potenziale, scorre corrente. Data la bassissima resistenza di un semplice filo, scorre tanta corrente. Data la relazione tra la potenza dissipata in calore e la corrente che attraversa il circuito, , viene dissipato tanto calore. Il circuito prende fuoco 🔥.
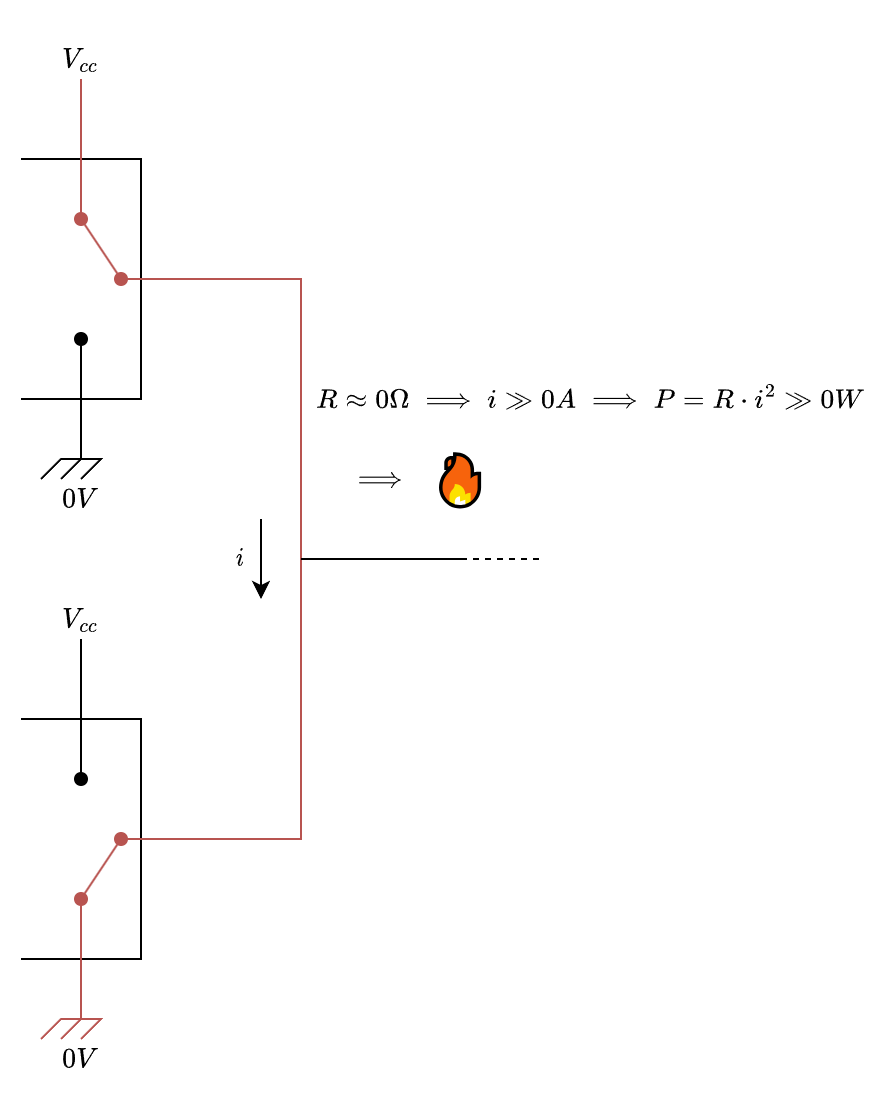
Arriviamo quindi al perché questo è un grosso problema all'esame:
in Verilog, questa regola si traduce in non si possono fare due o più assign allo stesso wire.
Questo è un errore tanto grave quanto è facile da fare, soprattutto se non si tiene a mente la corrispondenza con schemi circuitali come discusso sopra.
Per dar fuoco al proprio circuito basta infatti scrivere:
wire filo;
...
assign #1 filo = ...;
...
assign #1 filo = ...;
Una forma (purtroppo) comune di questo errore è quello in cui si tenta di usare un wire come variabile accumulatore.
wire [7:0] filo;
...
rete_combinatoria rc_1 (
.ingresso1(...), .ingresso2(...),
.uscita(filo)
)
rete_combinatoria rc_2 (
.ingresso1(...), .ingresso2(...),
.uscita(filo)
)
...
Ci sono qui due errori in tandem: si parte dall'idea che rc_1 e rc_2 lavorino in sequenza anziché in parallelo, come due righe distinte di un programma, e si arriva a collegare sia l'uscita di rc_1 che rc_2 allo stesso filo, creando il corto circuito.
Dall'uso del simulatore Verilog questo problema non è sempre evidente: se due valori assegnati sono gli stessi, il simulatore "lascia fare" assegnando quel valore al filo, se invece i valori sono distinti il filo avrà valore logico indeterminato 1'bx.
Uso efficiente di VS Code
Questa parte della lezione copre l'uso efficiente di VS codice. Il materiale relativo si trova qui.
Esercizi d'esame
Negli esercizi d'esame dove compare la sintesi di reti combinatorie, questa è parte di un esercizio più ampio: si chiede di realizzare una rete sincronizzata che interagisce con l'esterno per raccogliere input, svolgere un calcolo, e inviare un risultato. Viene chiesto di implementare tale calcolo con una rete combinatoria, da sintetizzare come modulo a parte utilizzato dalla rete sincronizzata.
Per esercitarsi, è possibile utilizzare tutti i testi d'esame in questa forma prendendo in considerazione solo la parte relativa alla rete combinatoria e ignorando, per ora il resto. Uno svantaggio è il fatto che le testbench fornite sono relative all'esercizio per intero, interfacciandosi solo con la rete sincronizzata, e si dovrà realizzare da sé una testbench apposita per testare la sola rete combinatoria.
Non è ancora pronta, ma prevista, una guida adeguata alle testbench preparate per gli esercizi d'esame e come riadattarle per altri usi, per esempio per testare solo la parte combinatoria.
Vediamo alcuni esercizi di reti combinatorie prese da testi d'esame.
Esercizio 2.1: parte combinatoria esame 2023-06-27
Qui il testo completo.
L'esercizio parla di una rete sincronizzata, che preleva due numeri naturali e , su 8 bit, e ha bisogno di calcolare .
Per ora, ci interessa soltanto la parte dove ci viene chiesto di sintetizzare la rete MAX che svolge questo calcolo.
Per testare tale rete, possiamo ricavarci una testbench come la seguente, scaricabile qui.
module testbench();
reg [7:0] x, y;
wire [7:0] z;
MAX m (
.x(x), .y(y), .max(z)
);
initial begin
x = 10; y = 5;
#10;
if(z != 10)
$display("Test failed!");
x = 5; y = 10;
#10;
if(z != 10)
$display("Test failed!");
x = 10; y = 10;
#10;
if(z != 10)
$display("Test failed!");
x = 100; y = 50;
#10;
if(z != 100)
$display("Test failed!");
x = 50; y = 100;
#10;
if(z != 100)
$display("Test failed!");
end
endmodule
Una versione più completa, ottenuta dalla testbench originale dell'esercizio prendendo lo schema del blocco consumer e i casi di test della funzione get_testcase, è scaricabile qui.
Notiamo che, come per le testbench d'esame, questa emette output solo in caso di errore.
Questo significa che quando lanciamo la simulazione, se vediamo a terminale solo le righe riguardo il file VCD e la $finish di fine simulaizone, possiamo dire che la testbench non ha trovato errori.
Questo non vuol dire che non ci sono, ed è sempre indicato di verificare da sé il corretto comportamento per tutti gli aspetti.
Vediamo ora il file reti_standard.v, anche questo fornito con l'esercizio.
Questo file contiene delle reti combinatorie che si assume note e sintetizzabili.
Ciò vuol dire che possiamo liberamente usarle come componenti nelle nostre sintesi di reti combinatorie - assieme alle porte logiche elementari e eventuali altre reti sintetizzate da noi nello stesso esercizio.
reti_standard.vIl contenuto di reti_standard.v varia da esercizio ad esercizio.
Questo sia in termini di reti fornite sia per la presenza o meno di parametri configurabili.
Ciò è intenzionale, e la difficoltà di un esercizio è data anche da ciò che si è fornito come partenza.
In questo caso abbiamo a disposizione una sola rete combinatoria, il sommatore.
Questo sommatore ha però un parametro, N.
I parametri sono simili ai generics nei linguaggi di programmazione: un modo per scrivere un modulo configurabile che si adatta a più situazioni, che in questo caso vuol dire a un diverso numero di bit.
Questo vuol dire che possiamo collocare nella nostra rete sommatori di qualunque numero di bit vogliamo, anzi dobbiamo trovare il numero giusto di bit da usare.
Prima di vedere la sintassi per usare queste reti parametriche, capiamo prima come lo vogliamo usare, ragionando sul problema con schemi circuitali. Una rete che determini il massimo tra due numeri dovrà necessariamente passare da una comparazione tra i due. Partiamo dall'idea di avere un comparatore il cui risultato fa da selettore per un multiplexer.
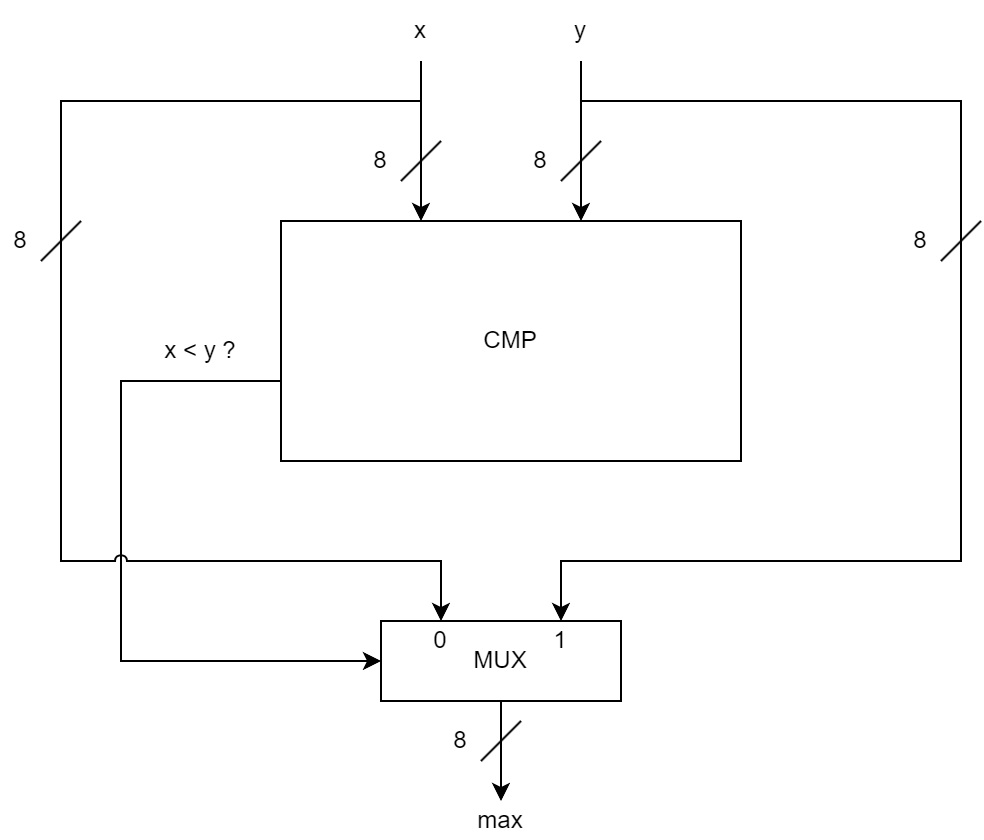
equivale a . Dato che e sono numeri naturali, questo equivale a chiedersi se la loro sottrazione genera un prestito uscente. Posso quindi realizzare questo comparatore usando un sottrattore.
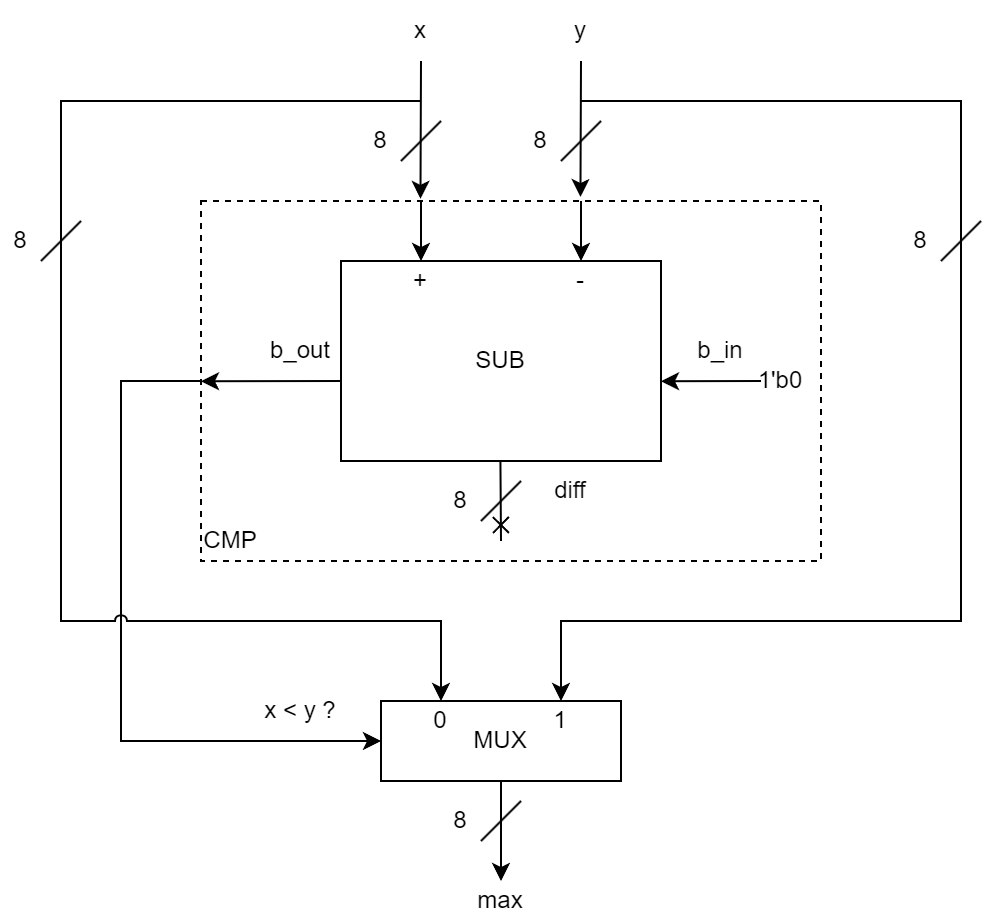
Arriviamo quindi a come fare il sottrattore: sappiamo dal modulo di aritmetica che si può fare a partire da un sommatore: basta negare il sottraendo e i riporti in ingresso e uscita.
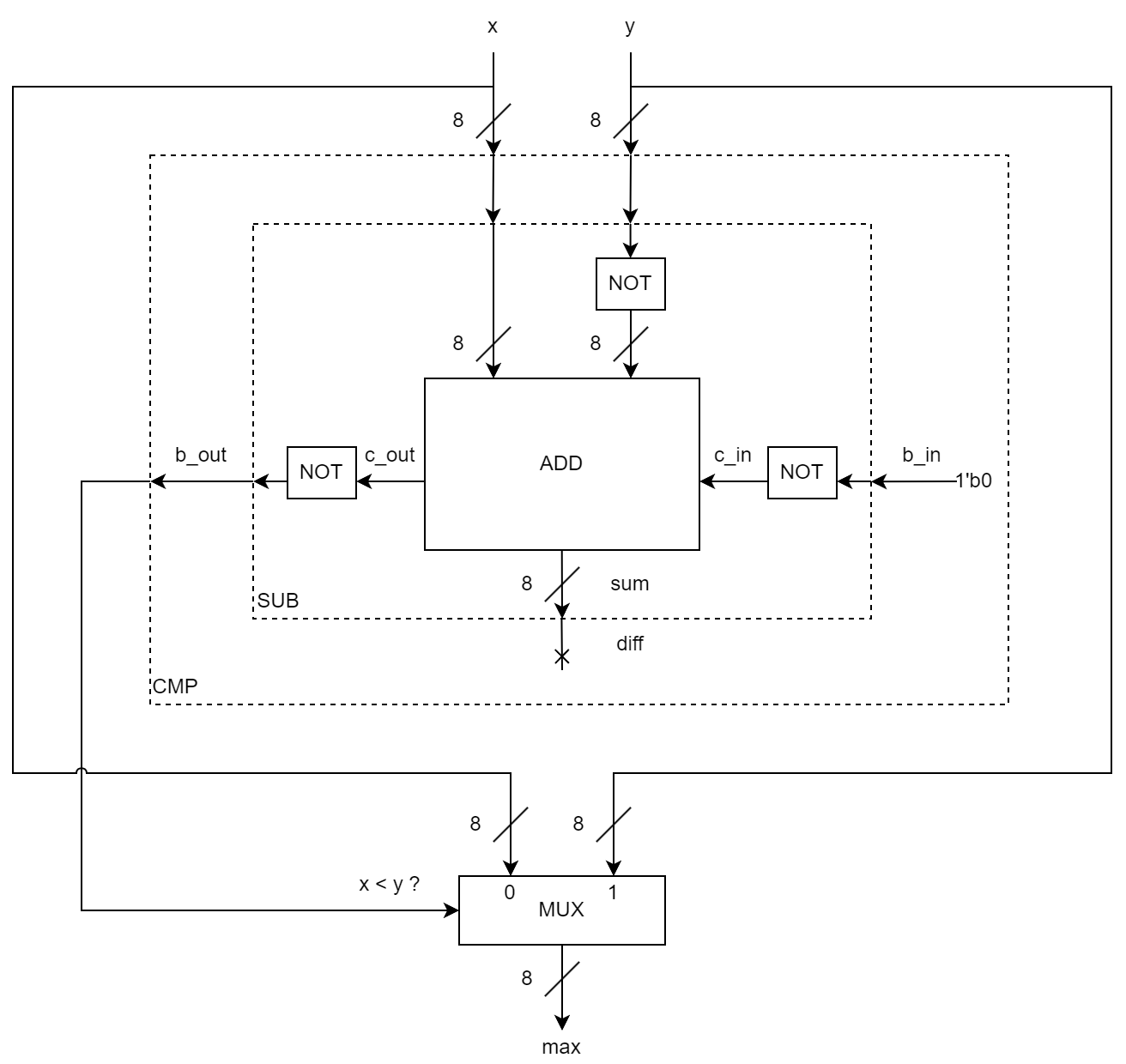
Abbiamo quindi una rete sintetizzabile: usiamo solo dei not, un multiplexer e un sommatore a 8 bit, quest'ultimo sintetizzabile perché parte della libreria reti_standard.v.
Possiamo ora scrivere l'equivalente in Verilog, specificando per il sommatore N = 8. Questo parametro viene impostato all'instanziazione del sommatore, e deve essere una costante: determina infatti la quantità di hardware utilizzata, e non si può cambiare l'hardware a runtime.
module MAX(
x, y,
max
);
input [7:0] x, y;
output [7:0] max;
wire [7:0] y_neg;
assign #1 y_neg = ~y;
wire c_out;
add #( .N(8) ) s (
.x(x), .y(y_neg), .c_in(1'b1),
.c_out(c_out)
);
wire b_out;
assign #1 b_out = ~c_out;
assign #1 max = b_out ? y : x;
endmodule
Esiste una certa flessibilità, soprattutto quando le reti si fanno più complesse, attorno alla sintesi esplicita con ritardi di operazioni come la negazione ~ e l'incremento +1.
Per esempio, in questo esercizio abbiamo dichiarato separatamente i wire y_neg e b_out, con dei ritardi negli assign relativi.
È lecito però anche evitare questi wire e scrivere più compattamente .y(~y) a riga 13 e ~c_out ? y : x a riga 20.
Uno svantaggio di questo approccio è che, rimuovemendo dei punti di ritardo, può rendere più difficile il debugging via waveform.
Esercizio 2.2: parte combinatoria esame 2023-01-31
Qui il testo completo.
Anche in questo caso, l'esercizio parla di una rete sincronizzata, che per ora ignoreremo. Per la rete sincronizzata, avremo da calcolare un prodotto di numeri naturali, ma abbiamo a disposizione solo mul+add da 4 bit (non parametrizzati).
Qui la testbench riadattata per la sola rete combinatoria.
Questo esercizio segue in realtà lo stesso schema dell'equivalente già visto in Assembler (qui), cambia solo la base, che passa da a . Anche se matematicamente è lo stesso problema, cambia abbastanza come dovremmo solgerlo proprio perché stiamo descrivendo hardware e non programmando software.
Soluzione 1
Una buona strategia, soprattutto quando si ha tempo limitato, è partire da soluzioni semplici ma funzionali, e passare poi a migliorarle.
Seguendo lo schema già visto, dovremo calcolare quattro sottoprodotti tra due cifre. Ciascun sottoprodotto può essere calcolato indipendentemente e produce un risultato su 2 cifre (8 bit). Questi sottoprodotti venivano shiftati a sinistra di 0, 1 o 2 cifre.
In Assembler, dopo questo passaggio si era già pronti a fare la somma su 4 cifre: questo perché i registri del processore hanno numeri di bit fissi, e le istruzioni a disposizione operano su questi numeri di bit. In Verilog, dove descriviamo hardware, i numeri di bit sono decisi da noi, ed è normale avere valori su numeri di bit diversi che non possiamo passare a un sommatore senza prima estenderli.
In altre parole, dobbiamo occuparci tanto degli zeri aggiunti a destra (per shift) quanto di quelli aggiunti a sinistra (per estensione) prima di poter sommare i sottoprodotti tra di loro. Una volta ottenuti i quattro sottoprodotti, tutti su 4 cifre, possiamo sommarli tra loro. Possiamo usare tre sommatori a 4 cifre (16 bit) per farlo. Otteniamo quindi lo schema seguente.
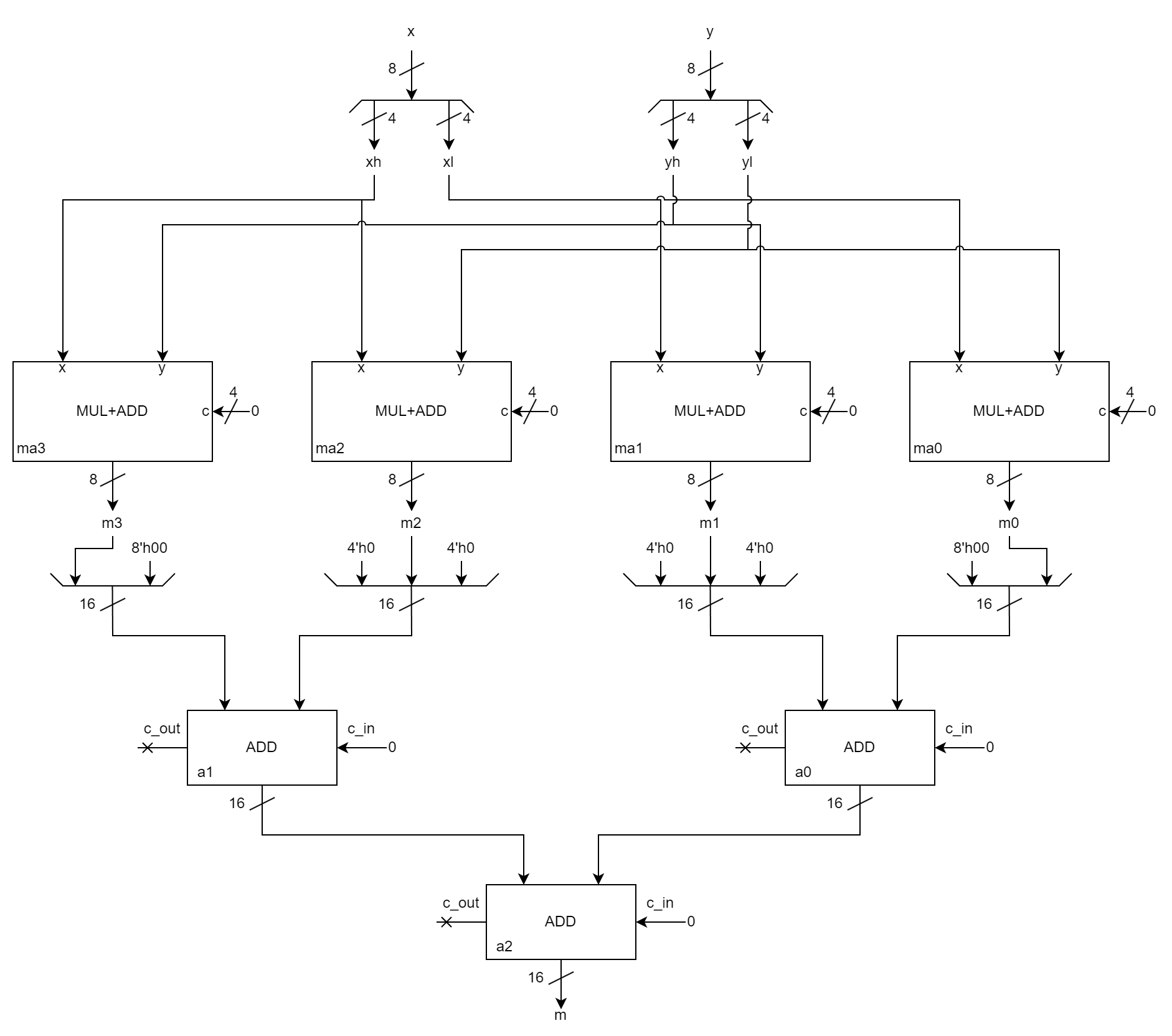
In Verilog, questo diventa quanto segue (scaricabile qui).
// x naturale su 8 bit
// y naturale su 8 bit
// m = x * y, su 16 bit
module MUL8(x, y, m);
input [7:0] x;
input [7:0] y;
output [15:0] m;
wire [3:0] xl, xh;
assign {xh, xl} = x;
wire [3:0] yl, yh;
assign {yh, yl} = y;
wire [7:0] m0;
mul_add_nat ma0(
.x(xl), .y(yl), .c(4'h0),
.m(m0)
);
wire [15:0] m0e = {8'h00, m0};
wire [7:0] m1;
mul_add_nat ma1(
.x(xl), .y(yh), .c(4'h0),
.m(m1)
);
wire [15:0] m1e = {4'h0, m1, 4'h0};
wire [7:0] m2;
mul_add_nat ma2(
.x(xh), .y(yl), .c(4'h0),
.m(m2)
);
wire [15:0] m2e = {4'h0, m2, 4'h0};
wire [7:0] m3;
mul_add_nat ma3(
.x(xh), .y(yh), .c(4'h0),
.m(m3)
);
wire [15:0] m3e = {m3, 8'h00};
wire [15:0] s0;
add #( .N(16) ) a0 (
.x(m0e), .y(m1e), .c_in(1'b0),
.s(s0)
);
wire [15:0] s1;
add #( .N(16) ) a1 (
.x(m2e), .y(m3e), .c_in(1'b0),
.s(s1)
);
add #( .N(16) ) a2 (
.x(s0), .y(s1), .c_in(1'b0),
.s(m)
);
endmodule
Questo è un esempio del tipo di esercizi dove è comune vedere confusione: dovendo sommare quattro valori, usando tre sommatori, si può pensare di poter utilizzare un wire come una variabile accumulatore.
Come spiegato, ciò non può funzionare in una rete combinatoria ed è un errore grave.
Soluzione 2
Nella soluzione precedente si può notare una inefficienza: abbiamo a disposizione solo reti mul+add, che hanno anche un ingresso c e calcolano , ma stiamo ignorando questa possibilità impostando tutti gli c a 0.
Per ottimizzare, possiamo quindi cercare un modo di sfruttare questi ingressi per ridurre il numero di sommatori. Ritorniamo alla somma in colonna dei sottoprodotti.
0 0 [ m0 ] +
0 [ m1 ] 0 +
0 [ m2 ] 0 +
[ m3 ] 0 0 +
Se guardiamo a m0, notiamo che la sua parte bassa è destinata a finire nella somma finale senza alcuna modifica, e dunque i sommatori sono, per quella parte, completamente superflui.
La stessa cosa accade per i bit più significativi, dove troviamo tanti zeri sommati tra di loro.
Per vedere meglio come procedere, scomponiamo anche i sottoprodotti in parte alta e parte bassa, per esempio {m0h, m0l} = m0.
0 0 m0h m0l +
0 m1h m1l 0 +
0 m2h m2l 0 +
m3h m3l 0 0 +
Ecco quindi le ottimizzazioni che si possono eseguire:
m0lnon viene sommato ad alcunché, dunquem[3:0] = m0lm0hpuò essere collegato all'inputcdima1oma2- sia
s0la sommam1 + m2 + m0h, scomposto in{s0h, s0l} = s0, ec0il suo eventuale riporto uscente. Alloram[7:4] = s0l, es0hpuò essere collegato all'inputcdima3. - sia
s1la sommam3 + s0h, scomposto in{s1h, s1l} = s1. Alloram[11:8] = s1l, mentrem[15:12] = s1h + c0.
Per realizzare questo ci serve, oltre ai moltiplicatori, un sommatore a 8 bit per s0, e un incrementatore a 4 bit per s1h + c0.
Lo schema che lo rappresenta è il seguente.
![Schema del moltiplicatore a 8 bit ottimizzato.
Utilizzando gli ingressi c e le scomposizioni, sono sufficienti un sommatore a 8 bit e un incrementatore a 4 bit.
Differenze con la prima soluzione:
'm0l' è collegato direttamente all'uscita 'm[3:0]';
'm0h' è collegato all'ingresso 'c' di 'ma1';
'ma1' produce 'm1 + m0h';
il sommatore a 8 bit 'a0' prende in ingresso 'm1 + m0h' e 'm2', produce 's0' e 'c0';
's0l' è collegato direttamente all'uscita 'm[7:4]';
's0h' è collegato all'ingresso 'c' di 'ma3';
'ma3' produce 's1 = m3 + s0h';
's1l' è collegato direttamente all'uscita 'm[11:8]';
l'incrementatore a 4 bit 'a1' calcola 's1h + c0', il cui risultato è collegato direttamente all'uscita 'm[15:12]'.](/reti-logiche-esercitazioni/2025-26/img/verilog/2/mul8-rc-2.drawio.png)
In Verilog, questo diventa quanto segue (scaricabile qui).
// x naturale su 8 bit
// y naturale su 8 bit
// m = x * y, su 16 bit
module MUL8(x, y, m);
input [7:0] x;
input [7:0] y;
output [15:0] m;
wire [3:0] xh, xl;
assign {xh, xl} = x;
wire [3:0] yh, yl;
assign {yh, yl} = y;
wire [7:0] m0;
mul_add_nat ma0(
.x(xl), .y(yl), .c(4'b0000),
.m(m0)
);
wire [3:0] m0h, m0l;
assign {m0h, m0l} = m0;
wire [7:0] m1_m0h;
mul_add_nat ma1(
.x(xl), .y(yh), .c(m0h),
.m(m1_m0h)
);
wire [7:0] m2;
mul_add_nat ma2(
.x(xh), .y(yl), .c(4'b0000),
.m(m2)
);
wire [7:0] s0;
wire c0;
add #( .N(8) ) a0 (
.x(m2), .y(m1_m0h), .c_in(1'b0),
.s(s0), .c_out(c0)
);
wire [3:0] s0h, s0l;
assign {s0h, s0l} = s0;
wire [7:0] m3_s0h;
mul_add_nat ma3(
.x(xh), .y(yh), .c(s0h),
.m(m3_s0h)
);
wire [3:0] s1h, s1l;
assign {s1h, s1l} = m3_s0h;
wire [3:0] s1h_c0;
add #( .N(4) ) a1 (
.x(s1h), .y(4'b0), .c_in(c0),
.s(s1h_c0)
);
assign m = {s1h_c0, s1l, s0l, m0l};
endmodule